Postoje tri boga: A, B i C. Zovu se Istina, Laž i Nasumičnost, ali vi ne znate koji se bog kako zove. Znate da Istina uvek govori istinu, Neistina stalno laže, a to da li će Nasumičnost govoriti istinu ili lagati u potpunosti je stvar slučajnosti. Vaš zadatak je da utvrdite ko je ko tako što ćete svakom bogu postaviti po samo jedno pitanje na koje se može odgovoriti sa „DA“ ili „NE“. Bogovi razumeju jezik kojim se služite, ali će na vaša pitanja odgovarati na svom jeziku: umesto „DA“ i „NE“, koristiće termine „Da“ i „Ja“, pri čemu vi ne znate šta koja od dve reči znači.
Pred vama je „Najteža logička zagonetka svih vremena“. Ukoliko vam pođe za rukom da je rešite pomoću tri pitanja, nemojte ostati na tome. U tom slučaju, vaš zadatak je da mozgalicu učinite još težom.
Ovu mozgalicu savremeni logičari tretiraju kao svoju omiljenu salonsku igru. Taj status ima od trenutka kada je Najteža logička zagonetka ikada prvi put tako nazvana – i rešena – od strane američkog logičara Džordža Bulosa (George Boolos), nedugo pre njegove smrti 1996. godine. Rešite je i malo bolje ćete znati kako da dođete do istine u svetu preplavljenom poluinformacijama. Usput, možda ćete nešto saznati i o samoj prirodi logike.
Bulos je uvek imao poseban pogled na svet. Jednom je održao javno predavanje o Gedelovoj (Kurt Gödel) drugoj teoremi nepotpunosti, jednom od najvećih dostignuća u matematičkoj logici, koristeći isključivo jednosložne reči. Viđan je kako šeta hodnicima Tehnološkog instituta u Masačusetstu (MIT), držeći u ruci nevidljivu kredu, kojom je na nevidljivoj tabli rešavao logičko-matematičke probleme.
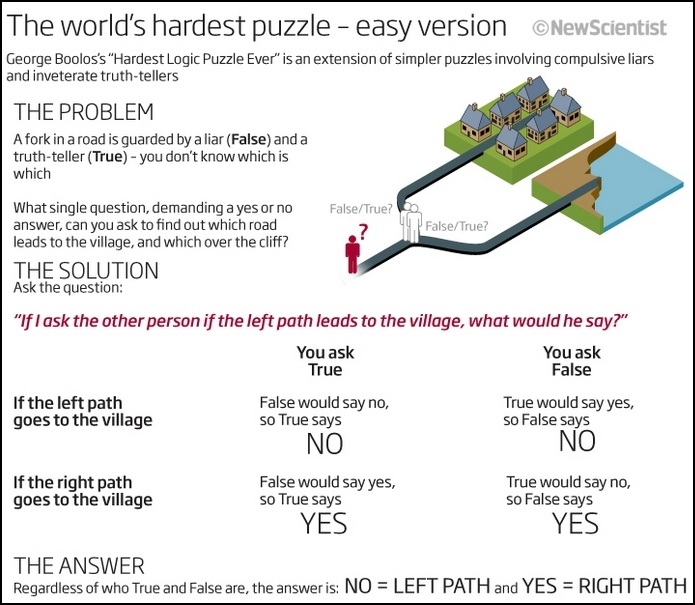
Gradeći Najtežu logičku zagonetku ikada, Bulos je pošao od serije mozgalica koje je popularizovao američki matematičar Rejmond Smulian (Raymond Smullyan). U Smulianovim slagalicama, nasukani ste se na obalu ostrva koje naseljavaju vitezovi koji uvek govore istinu i žandari koji stalno lažu. Imate mogućnost da postavite jedno pitanje kojim ćete od njih izvući informaciju od vitalne važnosti.
Bulosova genijalnost ogleda se u tome što je u mozgalicu ugradio više „detalja“ o koje se možete spotaći: (i) lažljivac i istinoljubac; (ii) ne znate jezik kojim govore; (iii) faktor slučajnosti. Time je ovaj logički zadatak učinio tako kompleksnim da ga je moguće rešiti jedino nizom vraški dobro osmišljenih pitanja.
Celokupno rešenje Najteže logičke zagonetke ikada Bulos je objavio u časopisu The Harvard Review of Philosophy. Ukoliko ste radi da uposlite mozak i probate da i sami dođete do njega, za sada nemojte otvarati ovaj link. Neka vam kao pomoć u potrazi za rešenjem posluži prvo od tri pitanja koja je Bulos postavio bogovima. Uputio ga je bogu A:
„Da li ‘Da’ znači ‘DA’ ako i samo ako si Istina, ako i samo ako je bog B Nasumičnost?“
Bulos se u formulisanje ovog logičkog zadatka nije upustio iz puke zabave. Njegovo rešenje počiva na širokoj upotrebi jednog od tri klasična aksioma formalne logike, koji se pripisuju Aristotelu. Poznat kao princip isključenja trećeg (srednjeg), on kaže da logička propozicija mora biti tačna ili netačna; treća mogućnost ili srednje rešenje ne postoji.
Postavlja se, međutim, pitanje da li je zakon isključenja trećeg sam po sebi istinit. Ako nije, da li je netačan? Razmotrimo, na primer, tvrdnju: „Aktuelni kralj Amerike nosi bradu.“ Da li je ova propozicija nužno netačna s obzirom da Amerika nema kralja ili leži negde u sivoj zoni između istine i neistinitosti? Svojim rešenjem Najteže zagonetke, Bulos teži da pokaže kako logički problemi postaju teški za rešavanje ukoliko se dopusti postojanje sredina.
Bulosovo rešenje nije bilo po svačijem ukusu. Tim Roberts (Tim Roberts), profesor logike na Univerzitetu Kvinslenda u Bundabergu, ocenio je, na primer, da zbog iskaza tipa „ako i samo ako“, na kojima je Bulos zasnovao svoje rešenje, laici logičare smatraju vrednim prezira. 2001. godine, Roberts je rešio Bulosovu mozgalicu bez upotrebe ovakvih iskaza, pokazujući da Najteža logička zagonetka i nije tako teška. Štaviše, predložio je dve još složenije alternative: (i) dva boga nose ime Nasumičnost, a treći je bilo Istina bilo Laž; (ii) jedan bog se zove Nasumičnost, a preostala dva su ili Istina ili Laž, pri čemu vam nije poznato koje od ta dva imena nose.
Pravi preokret nastupio je, međutim, 2008, kada su Brajan Rabern (Brian Rabern) i njegov brat Lendon (Landon) otkrili još fundamentalniju manu u Bulosovoj originalnoj postavci problema. Ona se ogleda u načinu na koji Nasumičnost daje odgovore. Prema pravilu koje je definisao Bulos, proces izgleda kao bacanje novčića, pri čemu glava znači da Nasumičnost govori istinu, a grb da laže. U tom slučaju, kažu braća Rabern, samo postavite pitanje „Da li ćeš lagati odgovarajući na ovo pitanje?“ Istina i Laž na ovako formulisano pitanje mogu da odgovore isključivo rečju koja znači „NE“. Zamislimo da Nasumičnost baca novčić pre nego što odgovori. Ako padne glava, govoriće istinu i moraće, takođe, da upotrebi reč koja znači „NE“. Ukoliko pak padne grb, moraće da laže, što znači da će ponovo upotrebiti reč koja u prevodu znači „NE“. Bilo kako bilo, jednim pitanjem otkrili ste kako se na jeziku bogova kaže „NE“.
Eksploziv za mozak
Manevar braće Rabern omogućava da se problem reši u tri iznenađujuće laka koraka. No, to nije sve. Istinu i Laž moguće je zbuniti samoreferentnim pitanjima (pitanjima na koja se odgovara iz prvog lica). Na primer, pitajte ih: „Da li ćeš na ovo pitanje odgovoriti sa ‘Ja’?“ Ako „Ja“ znači „NE“, Istina ne može da kaže istinu, a ukoliko znači „DA“, Laž ne može da izgovori laž. U svakom slučaju, jedan bog će ostati bez teksta.
Ovakvi nedovoljno definisani iskazi su propast za neoprezne programere, jer rezultiraju programima paralisanim usled neodlučnosti. Braća Rabern su, međutim, pokazali kako njihova promišljena upotreba vodi bržem otkrivanju Istine i Neistine i rešavanju zagonetke pomoću samo dva pitanja. Čak i kada je ponašanje Nasumičnosti podešeno da nasumice odgovara istinito, mozgalica je lako rešiva u tri koraka.
Braća Rabern nazvali su svoja pitanja pitanjima od kojih puca glava. Njihova validnost se preispituje (Explosive logic), ali su se u međuvremenu javile nove sumnje u validnost Bulosove zagonetke.
2010, Gabriel Uskiano (Gabriel Uzquiano), profesor filozofije na Oksfordu, iskoristio je „eksploziv za mozak“ da bi pokazao kako se uistinu nasumična verzija Najteže logičke zagonetke može rešiti pomoću samo dva pitanja. Potom je formulisao još težu verziju Bulosove mozgalice u kojoj Nasumičnost može nasumice da odluči da ćuti. Kasnije te godine, njegove kolege sa Karnegijevog Univerziteta u Pitsburgu, Gregori Viler (Gregory Wheeler) i Pedro Baraona (Pedro Barahona), obelodanili su rešenje za Uskianov problem koje se sastoji od seta od tri pitanja. I njih dvojica predložili su još kompleksniju mozgalicu; u njoj je Nasumičnost zamenjena bogom koji se zove Nepoštenje i koji kad god je u mogućnosti laže, ali se kada je zbunjen ponaša kao Nasumičnost.
Viler-Baraonina verzija mozgalice za sada je bez odgovora. Logičari, izvesno, rade na njenom rešenju, ali motivacija nije zabava, pa čak ni isključivo logika. Nasumičnost iz Bulosove zagonetke može se, naime, posmatrati kao model dolaženja do informacija iz izvora koji ne želi da ih oda, pa i kao model rezonovanja na bazi nepotpunih inforamcija, što je deo naše svakodnevice. Način na koji ih rešavamo može biti od pomoći u kreiranju veštačke inteligencije.
Šlag za tortu došao je iz Singapura, gde živi svetski poznati logičar-amater Nikolaj Novožilov (Nikolay Novozhilov). U njegovoj verziji zagonetke nije nam poznato ništa o jeziku kojim se bogovi služe kada odgovaraju. Dakle, da li je moguće rešiti je i u uslovima apsolutnog međusobnog nerazumevanja?
Pod uslovom da onaj kome se postavljaju pitanja na bilo koji način može da sugeriše distinkciju između logički fundamentalnih pojmova istinito i neistinito, moguće je.
Verzija Novožilova zadire pak u večnu debatu među lingvistima, koja se vodi oko pitanja šta su minimalni zahtevi koji moraju biti ispunjeni da bi se izgradio potpuno nov jezik. Ako se pitate zašto bi nam takav jezik bio potreban, Novožilov ima odgovor: Bio bi od pomoći u slučaju da sretnemo male zelene. Ideja je sledeća: Čak i da nemamo ni najmanju predstavu o tome kako neko komunicira, neki od aspekata te komunikacije biće nam jasni ukoliko imamo bazično razumevanje fenomena jezika kao takvog, tj. ako znamo šta je jezik zapravo.
Eksplozivna logika
Sada dolazimo na teren na kojem se pokazuje da Najteža logička zagonetka ikada, tačnije, put do njenog rešenja, ima implikacija po samu prirodu logike.
Bulosovo rešenje ticalo se principa isključenja trećeg. Rešenje zasnovano na pitanjima od kojih puca glava (pitanja na koja ne postoji istinit i neistinit odgovor) zadire pak u jedan drugi aksiom klasične logike. U pitanju je zakon ne-kontradikcije koji kaže da logička propozicija ne sme istovremeno da bude istinita i neistinita. „Eksplozivna“ logika kao da krši taj princip.
Jedan od njenih zastupnika, Grejem Prist (Graham Priest), logičar sa Gradskog Univerziteta u Njujorku, već tri decenije razvija „parakonzistentne“ logičke sisteme, koji dopuštaju istinite kontradikcije. Grejemova početna motivacija bilo je hvatanje u koštac s 2.500 godina starim paradoksom lažljivca – iskazima poput: „Ova tvrdnja je neistinita“ ili „Ja sada lažem.“
Parakonzistentna logika rešava probleme poput lažljivca i sličnih paradoksa time što naprosto dopušta da neke tvrdnje budu istovremeno istinite i neistinite. Njeni zastupnici pozivaju se na kvantnu fiziku u kojoj jedna te ista stvar ne mora biti jedno ili drugo, već može biti pomalo od oboje. Oponentima se pak diže kosa na glavi od ideje da bi logika mogla postati „talac“ realma empirijskog. Ako, međutim, ostane nefleksibilna, onda neki problemi, poput Najteže zagonetke, nemaju rešenje.



Povratni ping: Tri boga – najteža mozgalica svih vremena | veljahudin
da li neko moze da mi kaze odgovor? 😀
Sviđa mi seSviđa mi se
Ema, imaš u tekstu par odgovora. Biraj. 😀
Sviđa mi seSviđa mi se
Da li znas koliko kilograma ima drvo krusaka,jabuka ili visanja
Sviđa mi seSviđa mi se
kako slova mogu da nam odgovore mozda zagonetka nema resenje
Sviđa mi seSviđa mi se